Monte Carlo Tree Search

Los algoritmos rollout son algoritmos de planificación en el momento de la decisión basados en el control de Monte Carlo aplicado a trayectorias simuladas que comienzan todas en el estado actual del entorno. Calculan los valores de acción para una política dada promediando los retornos de muchas trayectorias simuladas que comienzan con cada acción posible y luego siguen la política dada. Cuando las estimaciones del valor de la acción se consideran suficientemente precisas, se ejecuta la acción (o una de las acciones) que tenga el valor estimado más alto, después de lo cual el proceso se lleva a cabo nuevamente desde el siguiente estado resultante.

Producen estimaciones de Monte Carlo de los valores de acción sólo para cada estado actual y para una política dada, generalmente denominada política rollout.

El objetivo de un algoritmo de rollout es mejorar la política de rollout, no encontrar una política óptima.

En algunas aplicaciones, un algoritmo de rollout puede producir un buen rendimiento incluso si la política de rollout es completamente aleatoria. Pero el rendimiento de la política mejorada depende de las propiedades de la política de rollout y de la clasificación de las acciones producidas por las estimaciones de valor de Monte Carlo. La intuición sugiere que cuanto mejor sea la política de rollout y más precisas las estimaciones de valor, es probable que mejor sea la política producida por un algoritmo de rollout.

Esto implica importantes cambios porque mejores políticas de rollout generalmente implican que se necesita más tiempo para simular trayectorias suficientes para obtener buenas estimaciones de valor.

El método de búsqueda de árboles de Monte Carlo (MCTS, por sus siglas en inglés) es un ejemplo reciente y sorprendentemente exitoso de planificación en el momento de la toma de decisiones. En su base, MCTS es un algoritmo rollout como el descrito anteriormente, pero mejorado mediante la incorporación de un medio para acumular estimaciones de valor obtenidas de las simulaciones de Monte Carlo con el fin de dirigir sucesivamente las simulaciones hacia trayectorias más gratificantes.

El MCTS se ejecuta después de encontrar cada nuevo estado para seleccionar la acción del agente para ese estado; se ejecuta nuevamente para seleccionar la acción para el siguiente estado, y así sucesivamente. Como en un algoritmo de implementación, cada ejecución es un proceso iterativo que simula muchas trayectorias que comienzan desde el estado actual y continúan hasta un estado terminal (o hasta que el descuento hace que cualquier recompensa adicional sea insignificante como contribución al retorno). La idea central del MCTS es enfocar sucesivamente múltiples simulaciones comenzando en el estado actual extendiendo las porciones iniciales de trayectorias que han recibido altas evaluaciones de simulaciones anteriores. El MCTS no tiene que retener funciones de valor aproximado o políticas de una selección de acción a la siguiente, aunque en muchas implementaciones retiene valores de acción seleccionados que probablemente sean útiles para su próxima ejecución.

Las estimaciones de valores de Monte Carlo se mantienen solo para el subconjunto de pares de estado-acción que tienen más probabilidades de alcanzarse en unos pocos pasos, que forman un árbol con raíz en el estado actual. MCTS extiende el árbol de manera incremental agregando nodos que representan estados que parecen prometedores según los resultados de las trayectorias simuladas. Cualquier trayectoria simulada pasará por el árbol y luego saldrá de él en algún nodo hoja. Fuera del árbol y en los nodos hoja, se utiliza la política rollout para las selecciones de acciones, pero en los estados dentro del árbol es posible algo mejor. Para estos estados, tenemos estimaciones de valores para al menos algunas de las acciones, por lo que podemos elegir entre ellas utilizando una política informada, llamada política de árbol, que equilibra la exploración y explotación. Por ejemplo, la política de árbol podría seleccionar acciones utilizando una regla de selección $\epsilon$-greedy o UCB (Upper Bound Confidence).

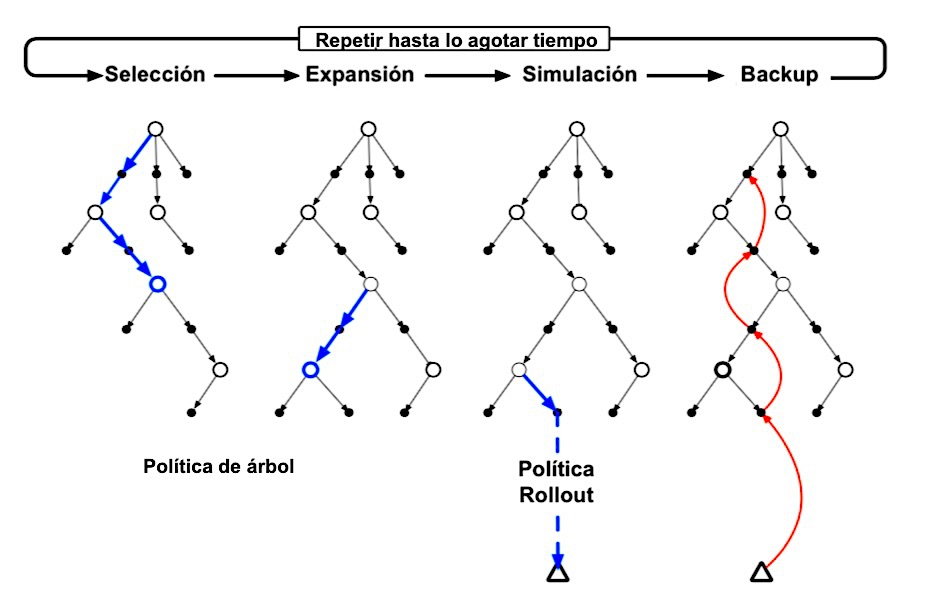
En más detalle, cada iteración de una versión básica de MCTS consta de los siguientes cuatro pasos

1. Selección. A partir del nodo raíz, una política de árbol basada en los valores de acción asociados a las aristas del árbol recorre el árbol para seleccionar un nodo hoja.

2. Expansión. En algunas iteraciones (según los detalles de la aplicación), el árbol se expande a partir del nodo de hoja seleccionado agregando uno o más nodos secundarios a los que se llega desde el nodo seleccionado mediante acciones no exploradas.

3. Simulación.(Rollout) Desde el nodo seleccionado, o desde uno de sus nodos secundarios recientemente agregados (si los hay), se ejecuta la simulación de un episodio completo con acciones seleccionadas por la política de rollout. El resultado es una prueba de Monte Carlo con acciones seleccionadas primero por la política de árbol y más allá del árbol por la política rollout.

4. Backup.(Retropropagación) El retorno generado por el episodio simulado se respalda para actualizar o inicializar los valores de acción asociados a las aristas del árbol recorrido por la política de árbol en esta iteración de MCTS. No se guardan valores para los estados y acciones visitados por la política de implementación más allá del árbol.

MCTS continúa ejecutando estos cuatro pasos, comenzando cada vez en el nodo raíz del árbol, hasta que no quede más tiempo o se agote algún otro recurso computacional. Luego, finalmente, se selecciona una acción del nodo raíz (que aún representa el estado actual del entorno) de acuerdo con algún mecanismo que depende de las estadísticas acumuladas en el árbol; por ejemplo, puede ser una acción que tenga el valor de acción más grande de todas las acciones disponibles desde el estado raíz, o quizás la acción con el mayor recuento de visitas para evitar seleccionar valores atípicos. Esta es la acción que MCTS realmente selecciona. Después de que el entorno pasa a un nuevo estado, MCTS se ejecuta nuevamente, a veces comenzando con un árbol de un solo nodo raíz que representa el nuevo estado, pero a menudo comenzando con un árbol que contiene cualquier descendiente de este nodo que quede del árbol construido por la ejecución anterior de MCTS; todos los nodos restantes se descartan, junto con los valores de acción asociados con ellos.

En su base, MCTS es un algoritmo de planificación en tiempo de decisión basado en el control de Monte Carlo aplicado a simulaciones que parten del estado raíz; es decir, es una especie de algoritmo rollout. Por tanto, se beneficia de la estimación de valor y la mejora de políticas en línea, incremental y basada en muestras.

La política del árbol o también llamada de selección. En un inicio esta política consistía en elegir aquel nodo (estado) que en promedio da más veces una recompensa, sin embargo, se han propuesto nuevas políticas de selección en las que destacan UCB y UCB-T.

Upper confidence bounds. Establece que la selección del nodo es aquel que maximice la ecuación $$UBC(S_i)={\bar{G}}_i+c\sqrt{\frac{LnN}{n_i}},$$ donde $c=2$,

${\bar{G}}_i$ es el promedio de recompensas obtenidas desde el estado $S_i$,

$n_i$ es el número de veces que se ha visitado el nodo $S_i$ hasta el momento,

$N$ es el número de veces que sea iterado.

El término ${\bar{G}}_i$ se encarga del proceso de explotación y el término $c\sqrt{\frac{LnN}{n_i}}$ del proceso de exploración. Durante la ejecución se puede ver que conforme un nodo es elegido más veces, el término de exploración deja de influir y el de explotación incrementa su influencia, lo que permite que UCB explore todas los nodos.

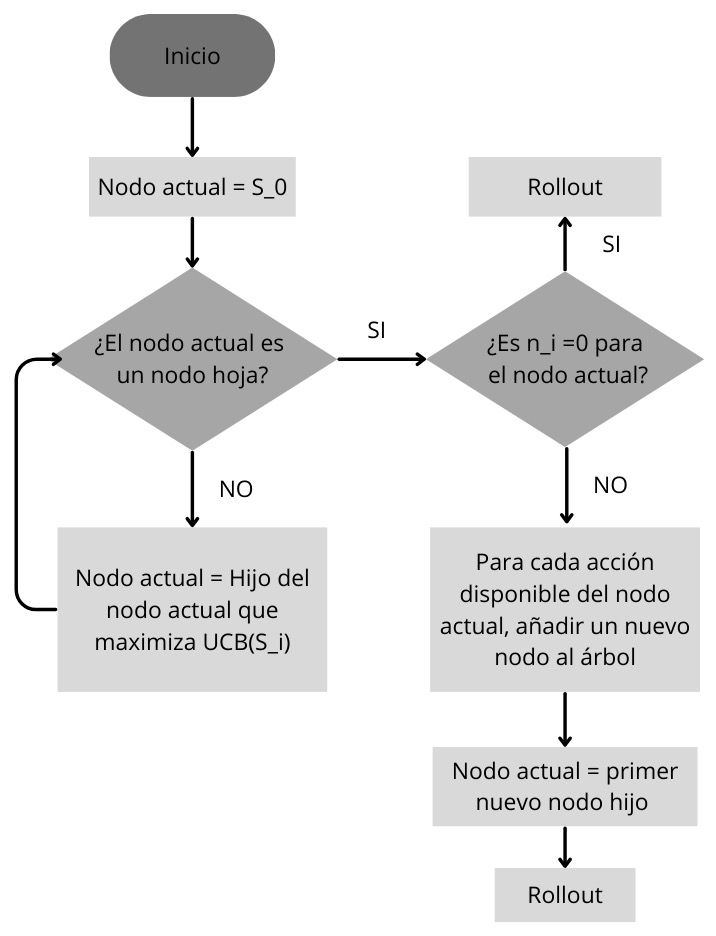
Simulación o también llamada rollout en inglés.

Donde $rollou{t}_{-}policy$ es la política de rollout que podría ser una política aleatoria o alguna política conveniente, para $simulate$ se requiere conocer la función de trasición de estados del ambiente. Y se supone que se trata un MDP episódico por lo cual se llega siempre a un estado terminal.

En otras palabras generamos un episodio siguiendo la política mencionada $S_i,A_i,S_{i+1},A_{i+1},\dots ,S_{T-1},A_{T-1},S_T$. Y $valor(S_T)=Recompensa$.

En cada nodo en el árbol $S_i$ guardamos dos valores $n_i$ que es el número de visitas al nodo $S_i$ y $t_i$ es la suma de las recompensas obtenidas desde $S_i$ hasta el momento, así ${\bar{G}}_i=t_i/n_i$. Notemos que para $S_0$, $n_0=N$.

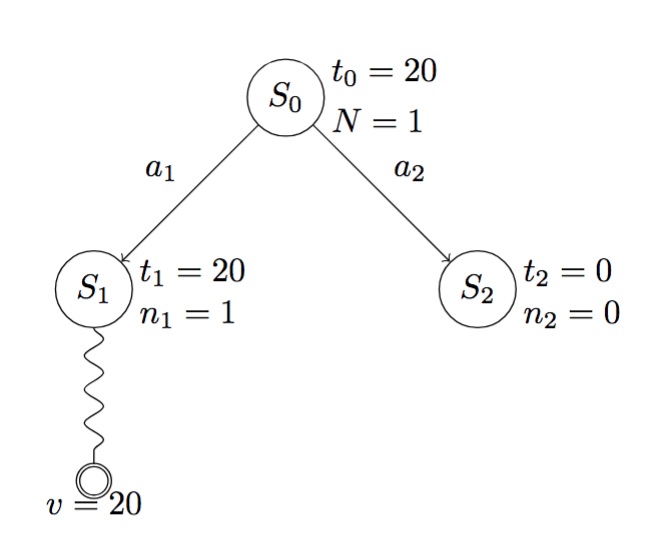
En el siguiente diagrama se muestra un ejemplo de la primera iteración: