Muchos sistemas e interacciones (redes sociales, moléculas, organizaciones, citas, modelos físicos, transacciones) pueden representarse de forma bastante natural como grafos. ¿Cómo podemos razonar sobre estos sistemas y hacer predicciones dentro de ellos?
Una idea es observar herramientas que han funcionado bien en otros dominios: las redes neuronales han demostrado un inmenso poder predictivo en una variedad de tareas de aprendizaje. Sin embargo, las redes neuronales se han utilizado tradicionalmente para operar con entradas de tamaño fijo y/o estructuradas regularmente (como oraciones, imágenes y videos). Esto las hace incapaces de procesar de forma elegante datos estructurados como grafos.
Las redes neuronales de grafos (GNN) son una familia de redes neuronales que pueden operar de manera natural sobre datos estructurados en grafos. Al extraer y utilizar características del grafo subyacente, las GNN pueden hacer predicciones más informadas sobre las entidades en estas interacciones, en comparación con los modelos que consideran entidades individuales de manera aislada.
Las GNN no son las únicas herramientas disponibles para modelar datos estructurados en grafos: los núcleos de grafos y los métodos de recorrido aleatorio fueron algunos de los más populares. Sin embargo, hoy en día, las GNN han reemplazado en gran medida a estas técnicas debido a su flexibilidad inherente para modelar mejor los sistemas subyacentes.
En este artículo, ilustraremos los desafíos de la computación sobre grafos, describiremos el origen y el diseño de las redes neuronales de grafos y exploraremos las variantes de GNN más populares en los últimos tiempos. En particular, veremos que muchas de estas variantes están compuestas por bloques de construcción similares.
¿Qué tipos de problemas tienen los datos estructurados como grafos?
Hemos descrito algunos ejemplos de gráficos en la naturaleza, pero ¿qué tareas queremos realizar con estos datos? Hay tres tipos generales de tareas de predicción en gráficos: a nivel de grafo, a nivel de nodo y a nivel de borde.
En una tarea a nivel de grafo, predecimos una sola propiedad para un grafo completo. Para una tarea a nivel de nodo, predecimos alguna propiedad para cada nodo en un grafo. Para una tarea a nivel de borde, queremos predecir la propiedad o presencia de bordes en un grafo.
Para los tres niveles de problemas de predicción descritos anteriormente (a nivel de grafo, a nivel de nodo y a nivel de borde), demostraremos que todos los siguientes problemas se pueden resolver con una sola clase de modelo, la GNN. Pero primero, hagamos un recorrido por las tres clases de problemas de predicción de grafos con más detalle y proporcionemos ejemplos concretos de cada uno.
Tarea a nivel de grafo
En una tarea a nivel de grafo, nuestro objetivo es predecir la propiedad de un grafo completo. Por ejemplo, para una molécula representada como un grafo, podríamos querer predecir a qué huele la molécula o si se unirá a un receptor implicado en una enfermedad.
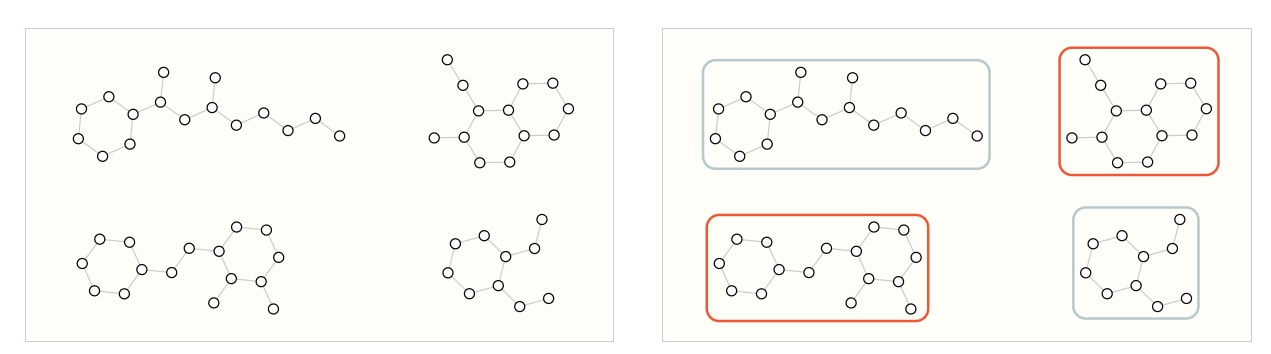Esto es análogo a los problemas de clasificación de imágenes con MNIST y CIFAR, donde queremos asociar una etiqueta a una imagen completa. Con el texto, un problema similar es el análisis de sentimientos, donde queremos identificar el estado de ánimo o la emoción de una oración completa a la vez.
Tarea a nivel de nodo
Las tareas a nivel de nodo se ocupan de predecir la identidad o el rol de cada nodo dentro de un gráfico.
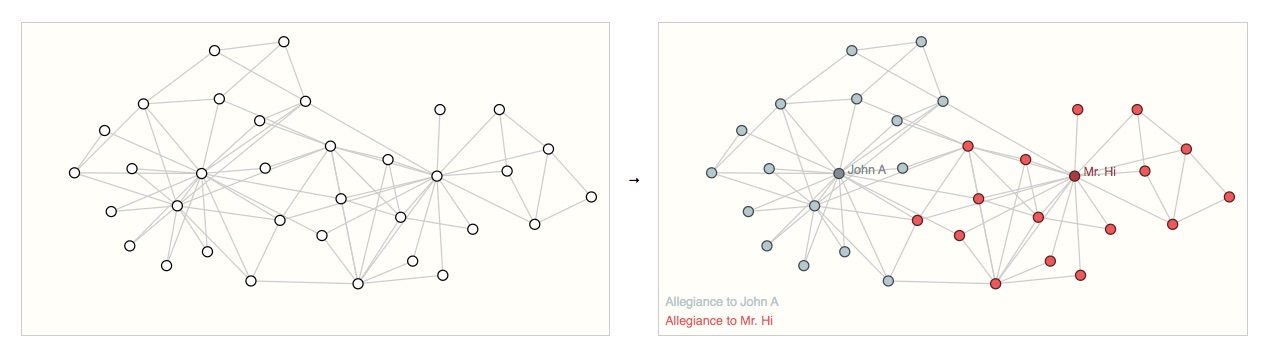
Un ejemplo clásico de un problema de predicción a nivel de nodo es el club de karate de Zach.
El conjunto de datos es un grafo de red social único formado por individuos que han jurado lealtad a uno de los dos clubes de karate después de una ruptura política. Según cuenta la historia, una disputa entre el Sr. Hi (instructor) y John H (administrador) crea un cisma en el club de karate. Los nodos representan a los practicantes de karate individuales y los bordes representan las interacciones entre estos miembros fuera del karate. El problema de predicción es clasificar si un miembro determinado se vuelve leal al Sr. Hi o a John H, después de la disputa. En este caso, la distancia entre un nodo y el Instructor o el Administrador está altamente correlacionada con esta etiqueta.
Siguiendo la analogía de la imagen, los problemas de predicción a nivel de nodo son análogos a la segmentación de imágenes, donde intentamos etiquetar el papel de cada píxel en una imagen. Con el texto, una tarea similar sería predecir las partes del discurso de cada palabra en una oración (por ejemplo, sustantivo, verbo, adverbio, etc.).
Tarea a nivel de borde
El problema de predicción restante en los grafos es la predicción de bordes.
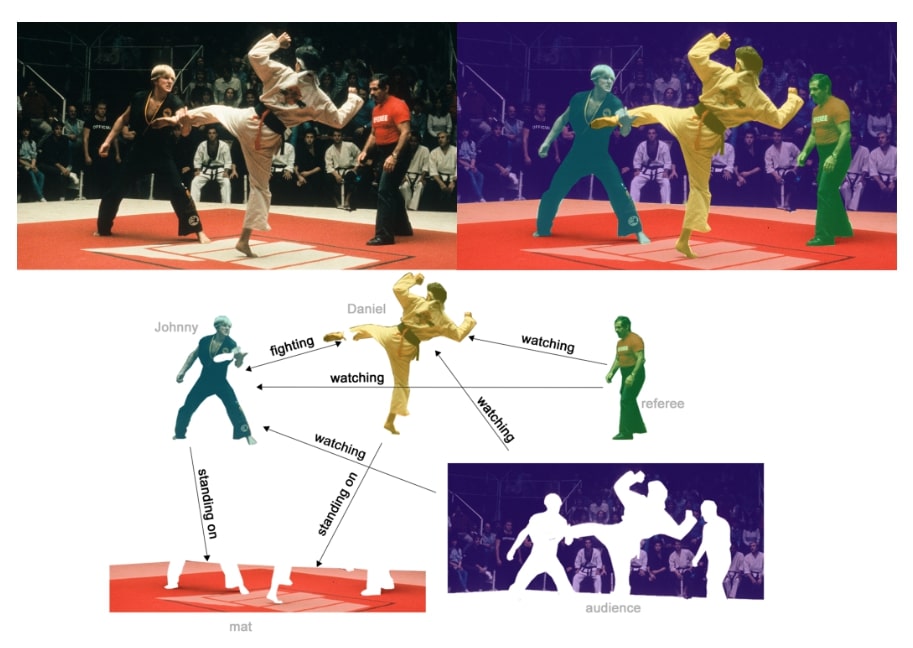
Un ejemplo de inferencia a nivel de borde es la comprensión de la escena de una imagen. Más allá de identificar objetos en una imagen, los modelos de aprendizaje profundo se pueden utilizar para predecir la relación entre ellos. Podemos expresar esto como una clasificación a nivel de borde: dados los nodos que representan los objetos en la imagen, deseamos predecir cuáles de estos nodos comparten un borde o cuál es el valor de ese borde. Si deseamos descubrir conexiones entre entidades, podríamos considerar que el grafo está completamente conectado y, en función de su valor predicho, podar los bordes para llegar a un grafo disperso.
Los desafíos del uso de grafos en el aprendizaje automático
Entonces, ¿cómo abordamos la solución de estas diferentes tareas de grafos con redes neuronales? El primer paso es pensar en cómo representaremos los grafos para que sean compatibles con las redes neuronales.
Los modelos de aprendizaje automático suelen tomar matrices rectangulares o similares a cuadrículas como entrada. Por lo tanto, no resulta inmediatamente intuitivo cómo representarlas en un formato que sea compatible con el aprendizaje profundo. Los grafos tienen hasta cuatro tipos de información que potencialmente querremos usar para hacer predicciones: nodos, aristas, contexto global y conectividad. Los primeros tres son relativamente sencillos: por ejemplo, con los nodos podemos formar una matriz de características de nodos
Sin embargo, representar la conectividad de un gráfico es más complicado. Quizás la opción más obvia sería usar una matriz de adyacencia, ya que esta es fácilmente tensorizable. Sin embargo, esta representación tiene algunas desventajas. Vemos que la cantidad de nodos en un grafo puede ser del orden de millones y la cantidad de aristas por nodo puede ser muy variable. A menudo, esto conduce a matrices de adyacencia muy dispersas, que son ineficientes en términos de espacio.
Otro problema es que hay muchas matrices de adyacencia que pueden codificar la misma conectividad y no hay garantía de que estas diferentes matrices produzcan el mismo resultado en una red neuronal profunda (es decir, no son invariantes a la permutación).
Una forma elegante y que ahorra memoria de representar matrices dispersas es como listas de adyacencia. Estas describen la conectividad de la arista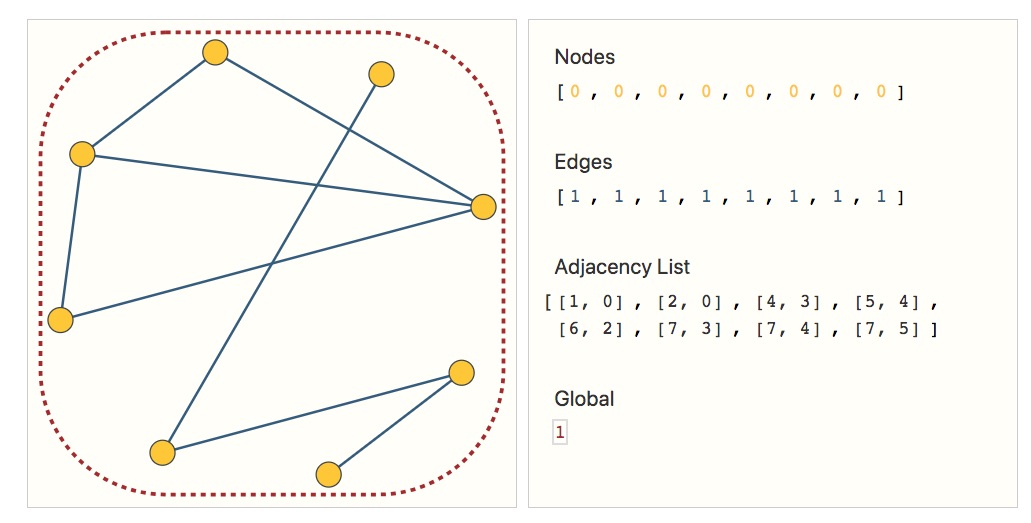 
Graph Neural Networks
Ahora que la descripción del grafos está en un formato de matriz que es invariante a la permutación, describiremos el uso de redes neuronales de grafos (GNN) para resolver tareas de predicción de grafos. Una GNN es una transformación optimizable en todos los atributos del grafo (nodos, aristas, contexto global) que preserva las simetrías del grafo (invariancias de permutación). Vamos a construir GNN utilizando el marco de “red neuronal de paso de mensajes” propuesto en el árticulo Neural Message Passing for Quantum Chemistry utilizando los esquemas de arquitectura de Graph Nets introducidos en Relational inductive biases, deep learning, and graph networks.
Las GNN adoptan una arquitectura de “grafo de entrada, grafo de salida”, lo que significa que estos tipos de modelos aceptan un grafo como entrada, con información cargada en sus nodos, aristas y contexto global, y transforman progresivamente estas incrustaciones, sin cambiar la conectividad del grafo de entrada.
La GNN más simple
Con la representación numérica de los grafos que hemos construido anteriormente (con vectores en lugar de escalares), ahora estamos listos para construir una GNN. Comenzaremos con la arquitectura GNN más simple, una en la que aprendemos nuevas incrustaciones para todos los atributos del gráfico (nodos, bordes, global), pero donde aún no usamos la conectividad del grafo.
Para simplificar, los diagramas anteriores usaban escalares para representar los atributos del gráfico; en la práctica, los vectores de características, o incrustaciones, son mucho más útiles. Esta GNN usa un perceptrón multicapa (MLP) independiente (o su modelo diferenciable favorito) en cada componente de un gráfico; lo llamamos una capa GNN. Para cada vector de nodo, aplicamos el MLP y obtenemos un vector de nodo aprendido. Hacemos lo mismo para cada borde, aprendiendo una incrustación por borde, y también para el vector de contexto global, aprendiendo una única incrustación para todo el grafo.
Como es habitual con los módulos o capas de redes neuronales, podemos apilar estas capas de GNN.
Como una GNN no actualiza la conectividad del gráfico de entrada, podemos describir el gráfico de salida de una GNN con la misma lista de adyacencia y la misma cantidad de vectores de características que el gráfico de entrada. Pero el gráfico de salida tiene incrustaciones actualizadas, ya que la GNN ha actualizado cada una de las representaciones de nodos, bordes y contexto global.
Predicciones de GNN mediante la agrupación de información
Hemos creado una red neuronal global simple, pero ¿cómo hacemos predicciones en cualquiera de las tareas que describimos anteriormente?
Consideraremos el caso de la clasificación binaria, pero este marco se puede extender fácilmente al caso de regresión o de clases múltiples. Si la tarea consiste en hacer predicciones binarias sobre nodos y el grafo ya contiene información de nodos, el enfoque es sencillo: para cada incrustación de nodos, se aplica un clasificador lineal.
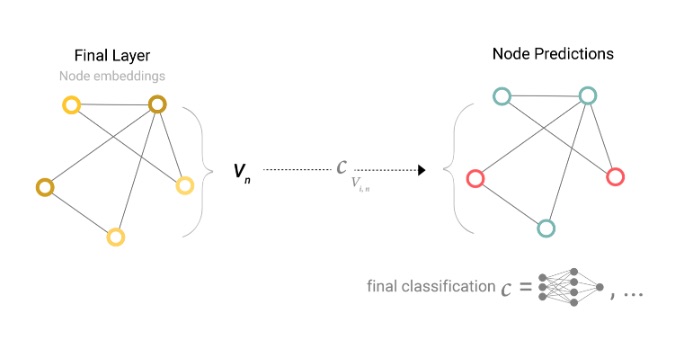
Sin embargo, no siempre es tan sencillo. Por ejemplo, puede que tenga información en el gráfico almacenada en los bordes, pero no en los nodos, pero aun así necesite hacer predicciones sobre los nodos. Necesitamos una forma de recopilar información de los bordes y dársela a los nodos para la predicción. Podemos hacerlo mediante la agrupación. La agrupación se lleva a cabo en dos pasos:
1. Para cada elemento que se va a agrupar, se reúnen todas sus incrustaciones y se concatenan en una matriz.
2. Las incrustaciones reunidas se agregan, normalmente mediante una operación de suma.
Representamos la operación de agrupación con la letra
Por lo tanto, si solo tenemos características a nivel de borde y estamos tratando de predecir la información de nodos binarios, podemos usar la agrupación para enrutar (o pasar) la información a donde debe ir. El modelo se ve así.
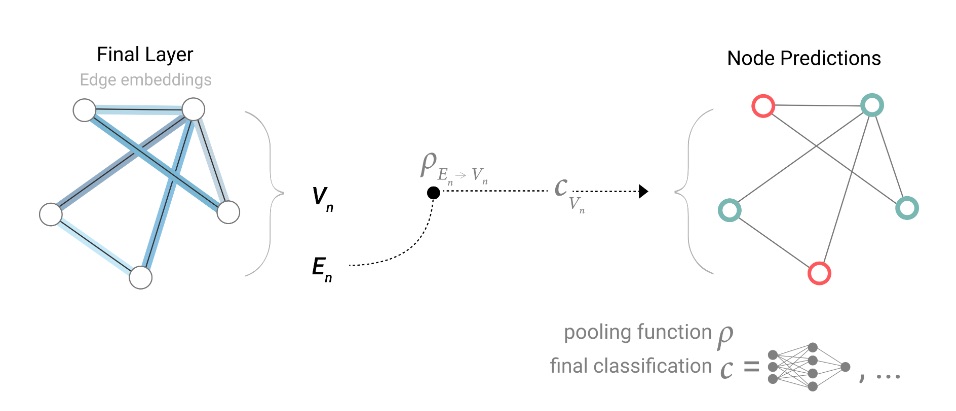
Si solo tenemos características a nivel de nodo y estamos tratando de predecir información binaria a nivel de borde, el modelo se ve así.
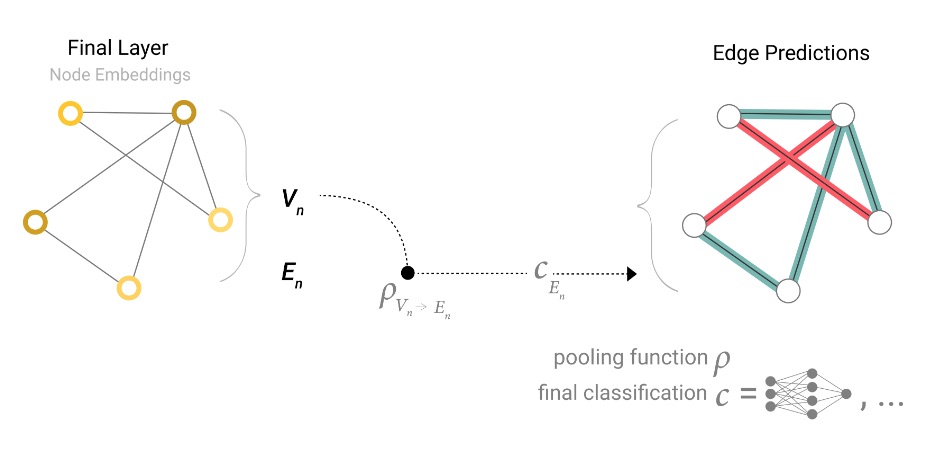
Si solo tenemos características a nivel de nodo y necesitamos predecir una propiedad global binaria, debemos reunir toda la información de nodo disponible y agregarla. Esto es similar a las capas de agrupación de promedios globales en las redes neuronales convolucionales. Lo mismo se puede hacer para los bordes.
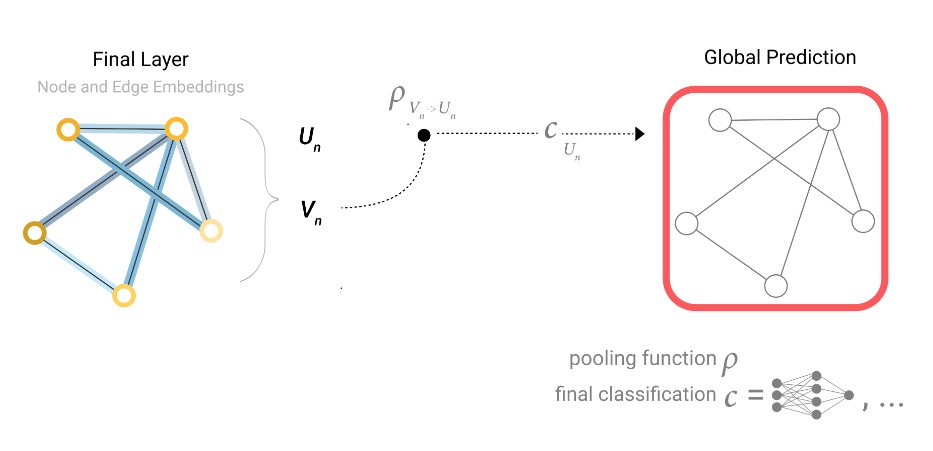
En nuestros ejemplos, el modelo de clasificación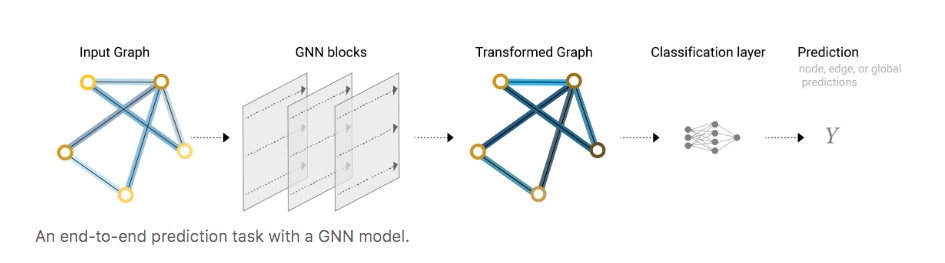 
Ahora hemos demostrado que podemos construir un modelo GNN simple y hacer predicciones binarias al enrutar información entre diferentes partes del gráfico. Esta técnica de agrupamiento servirá como un bloque de construcción para construir modelos GNN más sofisticados. Si tenemos nuevos atributos de gráfico, solo tenemos que definir cómo pasar información de un atributo a otro.
Tenga en cuenta que en esta formulación GNN más simple, no estamos utilizando la conectividad del gráfico en absoluto dentro de la capa GNN. Cada nodo se procesa de forma independiente, al igual que cada borde, así como el contexto global. Solo usamos la conectividad cuando agrupamos información para la predicción.
Pasar mensajes entre partes del grafo
Podríamos hacer predicciones más sofisticadas utilizando la agrupación dentro de la capa GNN, para que nuestras incrustaciones aprendidas sean conscientes de la conectividad del grafo. Podemos hacer esto utilizando el paso de mensajes, donde los nodos o bordes vecinos intercambian información e influyen en las incrustaciones actualizadas de los demás.
El paso de mensajes funciona en tres pasos:
1. Para cada nodo del grafo, reunir todas las incrustaciones (o mensajes) de los nodos vecinos, que es la función 𝑔 descrita anteriormente.
2. Agregar todos los mensajes a través de una función de agregación (como suma).
3. Todos los mensajes agrupados se pasan a través de una función de actualización, generalmente una red neuronal aprendida.
Así como la agrupación se puede aplicar a nodos o bordes, el paso de mensajes puede ocurrir entre nodos o bordes.
Estos pasos son clave para aprovechar la conectividad de los grafos. Construiremos variantes más elaboradas de paso de mensajes en capas GNN que produzcan modelos GNN de expresividad y potencia crecientes.
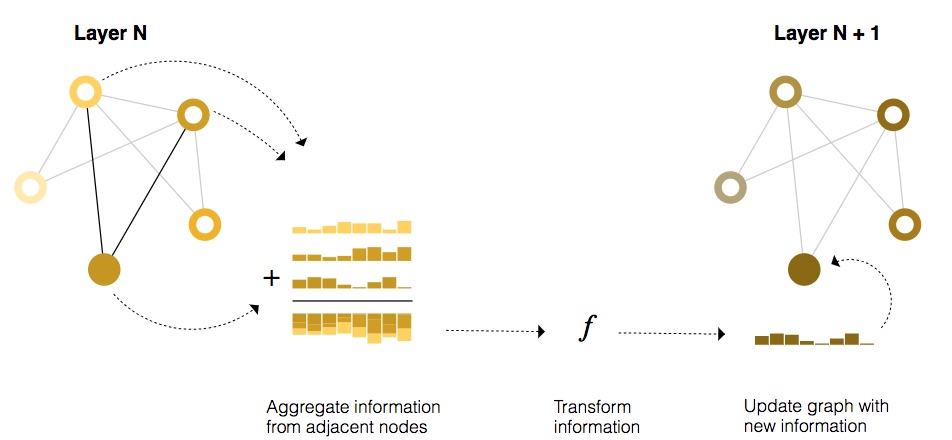Esta secuencia de operaciones, cuando se aplica una vez, es el tipo más simple de capa GNN de paso de mensajes.
Esto recuerda a la convolución estándar: en esencia, el paso de mensajes y la convolución son operaciones para agregar y procesar la información de los vecinos de un elemento con el fin de actualizar el valor del elemento. En los gráficos, el elemento es un nodo y, en las imágenes, el elemento es un píxel. Sin embargo, la cantidad de nodos vecinos en un gráfico puede ser variable, a diferencia de una imagen donde cada píxel tiene una cantidad determinada de elementos vecinos.
Al apilar capas GNN de paso de mensajes, un nodo puede eventualmente incorporar información de todo el gráfico: después de tres capas, un nodo tiene información sobre los nodos que se encuentran a tres pasos de distancia de él.
Representaciones de borde de aprendizaje
Nuestro conjunto de datos no siempre contiene todos los tipos de información (nodo, borde y contexto global). Cuando queremos hacer una predicción sobre nodos, pero nuestro conjunto de datos solo tiene información de borde, mostramos anteriormente cómo usar la agrupación para enrutar la información de los bordes a los nodos, pero solo en el paso de predicción final del modelo. Podemos compartir información entre nodos y bordes dentro de la capa GNN mediante el paso de mensajes.
Podemos incorporar la información de los bordes vecinos de la misma manera que usamos la información de los nodos vecinos anteriormente, primero agrupando la información del borde, transformándola con una función de actualización y almacenándola.
Sin embargo, la información de nodo y borde almacenada en un gráfico no tiene necesariamente el mismo tamaño o forma, por lo que no está claro de inmediato cómo combinarlos. Una forma es aprender un mapeo lineal del espacio de bordes al espacio de nodos y viceversa. Alternativamente, uno puede concatenarlos antes de la función de actualización.
Una de las decisiones de diseño que se deben tomar al construir redes neuronales globales es qué atributos de gráfico actualizamos y en qué orden lo hacemos. Podríamos elegir si actualizar las incrustaciones de nodos antes que las incrustaciones de aristas, o al revés. Esta es un área de investigación abierta con una variedad de soluciones; por ejemplo, podríamos actualizar en forma de “tejido”
donde tenemos cuatro representaciones actualizadas que se combinan en nuevas representaciones de nodos y aristas: nodo a nodo (lineal), arista a arista (lineal), nodo a arista (capa de aristas), arista a nodo (capa de nodos).
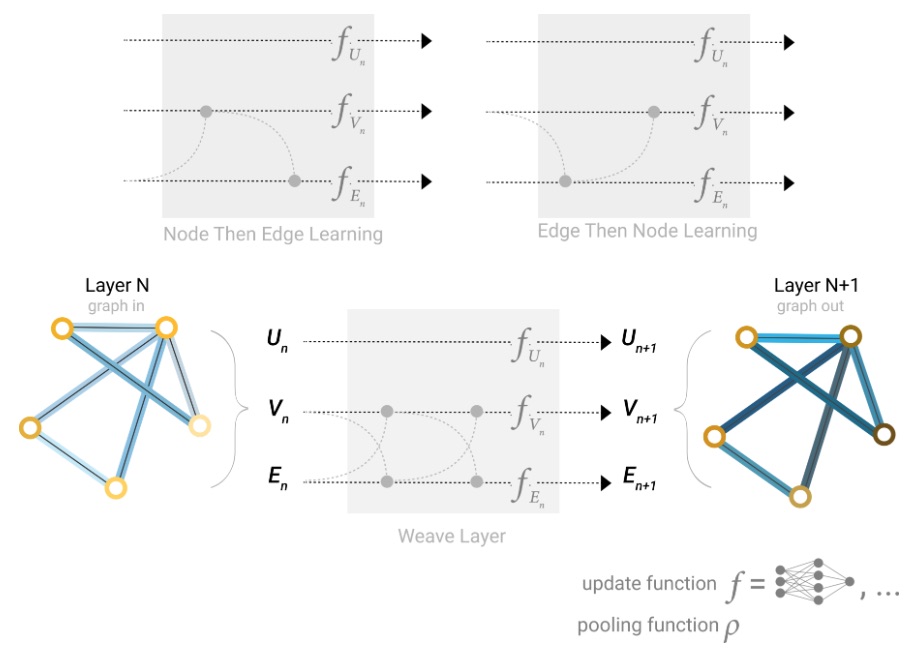
Añadiendo representaciones globales
Las redes que hemos descrito hasta ahora tienen un defecto: los nodos que están muy alejados entre sí en el gráfico pueden no ser capaces de transferirse información entre sí de forma eficiente, incluso si aplicamos el paso de mensajes varias veces. Para un nodo, si tenemos
Una solución a este problema es utilizar la representación global de un gráfico (
En esta vista, todos los atributos del grafo tienen representaciones aprendidas, por lo que podemos aprovecharlas durante la agrupación al condicionar la información de nuestro atributo de interés con respecto al resto. Por ejemplo, para un nodo podemos considerar la información de los nodos vecinos, los bordes conectados y la información global. Para condicionar la incorporación del nuevo nodo a todas estas posibles fuentes de información, podemos simplemente concatenarlas. Además, también podemos mapearlas al mismo espacio a través de un mapa lineal y agregarlas o aplicar una capa de modulación por características, que puede considerarse un tipo de mecanismo de atención por características.
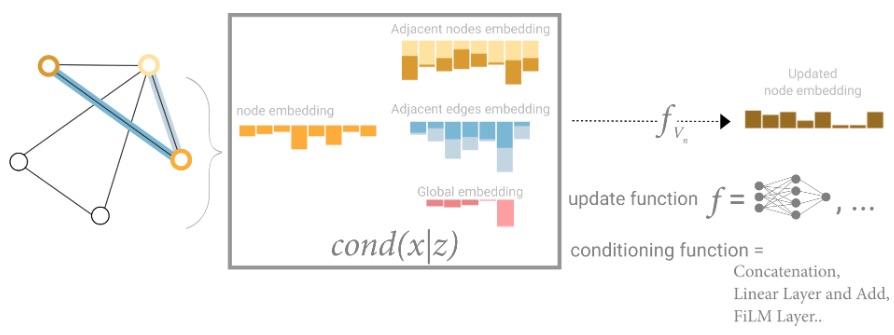
Referencias