Programación dinámica

El término programación dinámica (PD) se refiere a una colección de algoritmos que pueden utilizarse para calcular políticas óptimas dado un modelo perfecto del entorno como un proceso de decisión de Markov (PDM).

Los algoritmos DP clásicos son de utilidad limitada en el aprendizaje de refuerzo, tanto por su suposición de un modelo perfecto como por su gran gasto computacional, pero siguen siendo importantes teóricamente.

La idea clave del aprendizaje por refuerzo es el uso de funciones de valor para organizar y estructurar la búsqueda de buenas políticas. Veremos cómo se puede utilizar el aprendizaje por refuerzo para calcular las funciones de valor. Podemos obtener fácilmente políticas óptimas una vez que hayamos encontrado las funciones de valor óptimas, $v_{\ast }$ o $q_{\ast }$, que satisfacen las ecuaciones de optimalidad de Bellman, recordemos que: $$\begin{array}{rcl}{v}_{\ast }(s)& =& \underset{a}{max}\mathbb{E}[R_{t+1}+\gamma v_{\ast }(S_{t+1})|S_t=s,A_t=a]\\ & =& \underset{a}{max}\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma v_{\ast }(s^{\prime })]\text{ o }\\ q_{\ast }(s)& =& \mathbb{E}[R_{t+1}+\gamma \underset{a^{\prime }}{max}{q}_{\ast }(S_{t+1},a^{\prime })|S_t=s,A_t=a]\\ & =& \sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma \underset{a}{max}{q}_{\ast }(s^{\prime },a^{\prime })]\end{array}$$ Los algoritmos DP se obtienen convirtiendo ecuaciones de Bellman como éstas en asignaciones, es decir, en reglas de actualización para mejorar las aproximaciones de las funciones de valor deseado.

En primer lugar, analizamos cómo calcular la función de valor de estado $v_{\pi }$ para una política arbitraria $\pi$. Esto se denomina evaluación de políticas en la literatura sobre planificación de políticas. También lo denominamos problema de predicción. Sea $s\in \mathcal{S}$, recordemos que $$\begin{array}{rcl}{v}_{\pi }(s)& =& {\mathbb{E}}_{\pi }[G_t|S_t=s]\\ & =& {\mathbb{E}}_{\pi }[R_{t+1}+\gamma G_{t+1}|S_t=s]\\ & =& {\mathbb{E}}_{\pi }[R_{t+1}+\gamma v_{\pi }(S_{t+1}|S_t=s]\\ & =& \sum _a\pi (a|s)\sum _{s^{\prime },r^{\prime }}p(s^{\prime },r|s,a)[r+\gamma v_{\pi }(s^{\prime })],\end{array}$$ Si se conoce completamente la dinámica del entorno, entonces la última igualdad es un sistema de $|\mathcal{S}|$ ecuaciones lineales simultáneas con $|\mathcal{S}|$ incógnitas (las $v_{\pi }(s),s\in \mathcal{S})$. En principio, su solución es un cálculo sencillo, aunque tedioso. Para nuestros propósitos, los métodos de solución iterativos son los más adecuados.

Consideremos una secuencia de funciones de valor aproximado $v_0,v_1,v_2,\dots$, cada una de las cuales asigna $\mathcal{S}$ a $\mathbb{R}$. La aproximación inicial, $v_0$, se elige arbitrariamente (excepto que el estado terminal, si lo hay, debe tener el valor $0$), y cada aproximación sucesiva se obtiene utilizando la ecuación de Bellman para $v_{\pi }$ como regla de actualización: $$\begin{array}{rcl}{v}_{k+1}(s)& =& {\mathbb{E}}_{\pi }[R_{t+1}+\gamma v_k(S_{t+1})|S_t=s]\\ & =& \sum _a\pi (a|s)\sum _{s^{\prime },r^{\prime }}p(s^{\prime },r|s,a)[r+\gamma v_k(s^{\prime })],\end{array}$$ para todo $s\in \mathcal{S}$.

Se puede probar que la sucesión $\{v_k\}$ converge a $v_{\pi }$ cuando $k\to \mathrm{\infty }$ bajo las mismas condiciones que garantizan la existencia de $v_{\pi }$. Este algoritmo es llamado evaluación iterativa de política.

En el cuadro siguiente se muestra en pseudocódigo una versión completa de la evaluación iterativa de políticas. Observe cómo maneja la terminación. Formalmente, la evaluación iterativa de políticas converge solo en el límite, pero en la práctica debe detenerse antes de llegar a este punto. El pseudocódigo prueba la cantidad $ma{x}_{s\in \mathcal{S}}|v_{k+1}(s)-v_k(s)|$ después de cada barrido y se detiene cuando es lo suficientemente pequeña.

Nuestra razón para calcular la función de valor de una política es ayudar a encontrar mejores políticas. Supongamos que hemos determinado la función de valor $v_{\pi }$ para una política determinista arbitraria $\pi$. Para algún estado $s$ nos gustaría saber si deberíamos o no cambiar la política para elegir de manera determinista una acción $a\ne \pi (s)$. Sabemos lo bueno que es seguir la política actual desde $s$ (es decir, $v_{\pi }(s)$), pero ¿sería mejor o peor cambiar a la nueva política? Una forma de responder a esta pregunta es considerar la selección de $a$ en $s$ y a partir de entonces siguiendo la política existente, $\pi$. El valor de esta forma de comportarse es $$\begin{array}{rcl}{q}_{\pi }(s,a)& =& \mathbb{E}[R_{t+1}+\gamma v_{\pi }(S_{t+1})|S_t=s,A_t=a]\\ & =& \sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma v_{\pi }(s^{\prime })].\end{array}$$ El criterio clave es si esto es mayor o menor que $v_{\pi }(s)$.

Teorema de mejora de política. Sean $\pi$ y ${\pi }^{\prime }$ cualesquiera dos políticas deterministas tales que, para todo $s\in \mathcal{S}$, $$q_{\pi }(s,{\pi }^{\prime }(s))\ge v_{\pi }(s).$$ Entonces la política ${\pi }^{\prime }$ es tan buena o mejor que $\pi$. Así, para todos los estados $s\in \mathcal{S}$: $$v_{{\pi }^{\prime }}(s)\ge v_{\pi }(s).$$

Hasta ahora hemos visto cómo, dada una política y su función de valor, podemos evaluar fácilmente un cambio en la política en un solo estado para una acción particular. Es una extensión natural considerar los cambios en todos los estados y en todas las acciones posibles, seleccionando en cada estado la acción que parezca mejor según $q_{\pi }(s,a)$. En otras palabras, considerar la nueva política codiciosa, ${\pi }^{\prime }$, dada por $$\begin{array}{rcl}{\pi }^{\prime }(s)& =& \underset{a}{argmax}{q}_{\pi }(s,a)\\ & =& \underset{a}{argmax}\mathbb{E}[R_{t+1}+\gamma v_{\pi }(S_{t+1})|S_t=s,A_t=a]\\ & =& \underset{a}{argmax}\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma v_{\pi }(s^{\prime })],\end{array}$$

La política codiciosa adopta la acción que parece mejor en el corto plazo (después de un paso de previsión) de acuerdo con $v_{\pi }$. Por construcción, la política codiciosa cumple las condiciones del teorema de mejora de políticas, por lo que sabemos que es tan buena como, o mejor que, la política original. El proceso de crear una nueva política que mejore una política original, al hacerla codiciosa con respecto a la función de valor de la política original, se denomina mejora de políticas.

Por lo tanto, la mejora de la política debe darnos una política estrictamente mejor, excepto cuando la política original ya sea óptima.

Una vez que la política $\pi$ se ha mejorado usando $v_{\pi }$ para obtener una mejor política ${\pi }^{\prime }$, podemos calcular $v_{{\pi }^{\prime }}$ y mejorarla otra vez para obtener una política ${\pi }^{{}^{″}}$ aún mejor. Así es posible obtener una sucesión de políticas que mejoran monótonamente y funciones de valor: $${\pi }_0\stackrel{E}{⟶}{v}_{{\pi }_0}\stackrel{I}{⟶}{\pi }_1\stackrel{E}{⟶}{v}_{{\pi }_1}\stackrel{I}{⟶}{\pi }_2\stackrel{E}{⟶}\cdots \stackrel{I}{⟶}{\pi }_{\ast }\stackrel{E}{⟶}{v}_{\ast },$$ donde $\stackrel{E}{⟶}$ denota la evaluación de la política y $\stackrel{I}{⟶}$ denota la mejora de política.

Se garantiza que cada política será una mejora estricta de la anterior (a menos que ya sea óptima). Debido a que un MDP finito tiene solo una cantidad finita de políticas, este proceso debe converger hacia una política óptima y una función de valor óptima en una cantidad finita de iteraciones.

Esta forma de encontrar una política óptima se denomina iteración de políticas. En el cuadro siguiente se ofrece un algoritmo completo.

Una desventaja de la iteración de políticas es que cada una de sus iteraciones implica una evaluación de políticas, que puede ser en sí misma un cálculo iterativo prolongado que requiere múltiples barridos a través del conjunto de estados. Si la evaluación de políticas se realiza de manera iterativa, entonces la convergencia exacta a $v_{\pi }$ ocurre solo en el límite. ¿Debemos esperar a que se produzca la convergencia exacta o podemos detenernos antes de que eso ocurra?

De hecho, el paso de evaluación de políticas de la iteración de políticas se puede truncar de varias maneras sin perder las garantías de convergencia de la iteración de políticas. Un caso especial importante es cuando la evaluación de políticas se detiene después de un solo barrido (una actualización de cada estado). Este algoritmo se llama iteración de valor. Se puede escribir como una operación de actualización particularmente simple que combina los pasos de mejora de políticas y evaluación de políticas truncadas: $$\begin{array}{rcl}{v}_{k+1}(s)& =& \underset{a}{max}\mathbb{E}[R_{t+1}+\gamma v_k(S_{t+1})|S_t=s,A_t=a]\\ & =& \underset{a}{max}\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma v_k(s^{\prime })],\end{array}$$ para todo $s\in \mathcal{S}$. Para un arbitraria $v_0$, se puede probar que la sucesión $\{v_k\}$ converge a $V_{\ast }$ bajo las mismas condiciones que garantizan la existencia de $v_{\ast }$.

Otra forma de entender la iteración de valor es mediante la referencia a la ecuación de optimalidad de Bellman. Nótese que la iteración de valor se obtiene simplemente convirtiendo la ecuación de optimalidad de Bellman en una regla de actualización. Nótese también que la actualización de la iteración de valor es idéntica a la actualización de la evaluación de la política excepto que requiere que se tome el máximo en todas las acciones.

Por último, consideremos cómo termina la iteración de valor. Al igual que la evaluación de políticas, la iteración de valor requiere formalmente un número infinito de iteraciones para converger exactamente a $v_{\ast }$. En la práctica, nos detenemos una vez que la función de valor cambia solo una pequeña cantidad en un barrido. El cuadro a continuación muestra un algoritmo completo con este tipo de condición de terminación.

La iteración de valor combina efectivamente, en cada uno de sus barridos, un barrido de evaluación de políticas y un barrido de mejora de políticas. A menudo se logra una convergencia más rápida interponiendo múltiples barridos de evaluación de políticas entre cada barrido de mejora de políticas. En general, toda la clase de algoritmos de iteración de políticas truncadas se puede considerar como secuencias de barridos, algunos de los cuales utilizan actualizaciones de evaluación de políticas y otros de los cuales utilizan actualizaciones de iteración de valor.

Como la operación máxima en la ecuación es la única diferencia entre estas actualizaciones, esto simplemente significa que la operación máxima se agrega a algunos barridos de la evaluación de políticas. Todos estos algoritmos convergen a una política óptima para MDP finitos descontados.

Una desventaja importante de los métodos DP que hemos analizado hasta ahora es que implican operaciones sobre todo el conjunto de estados del MDP, es decir, requieren barridos del conjunto de estados. Si el conjunto de estados es muy grande, entonces incluso un solo barrido puede ser prohibitivamente costoso.

Por ejemplo, el juego de backgammon tiene más de ${10}^{20}$ estados. Incluso si pudiéramos realizar la actualización de iteración de valores en un millón de estados por segundo, se necesitarían más de mil años para completar un solo barrido.

Los algoritmos asíncronos son algoritmos iterativos en el lugar que no están organizados en términos de barridos sistemáticos del conjunto de estados. Estos algoritmos actualizan los valores de los estados en cualquier orden, utilizando los valores de otros estados que estén disponibles. Los valores de algunos estados pueden actualizarse varias veces antes de que los valores de otros se actualicen una vez.

Sin embargo, para converger correctamente, un algoritmo asíncrono debe continuar actualizando los valores de todos los estados: no puede ignorar ningún estado después de cierto punto en el cálculo. Los algoritmos asíncronos permiten una gran flexibilidad a la hora de seleccionar los estados que se actualizarán.

Por supuesto, evitar los barridos no significa necesariamente que podamos salirnos con la nuestra con menos cálculos. Simplemente significa que un algoritmo no necesita quedar atrapado en un barrido desesperanzadamente largo antes de poder avanzar en la mejora de una política. Podemos intentar aprovechar esta flexibilidad seleccionando los estados a los que aplicamos actualizaciones para mejorar la tasa de progreso del algoritmo. Podemos intentar ordenar las actualizaciones para permitir que la información de valores se propague de un estado a otro de manera eficiente. Es posible que algunos estados no necesiten que se actualicen sus valores con tanta frecuencia como otros. Incluso podríamos intentar omitir por completo la actualización de algunos estados si no son relevantes para el comportamiento óptimo.

Los algoritmos asincrónicos también facilitan la combinación de computación con interacción en tiempo real. Para resolver un MDP determinado, podemos ejecutar un algoritmo de DP iterativo al mismo tiempo que un agente está experimentando el MDP. La experiencia del agente se puede utilizar para determinar los estados a los que el algoritmo de DP aplica sus actualizaciones. Al mismo tiempo, la información más reciente sobre valores y políticas del algoritmo de DP puede guiar la toma de decisiones del agente.

Por ejemplo, podemos aplicar actualizaciones a los estados a medida que el agente los visita. Esto permite centrar las actualizaciones del algoritmo de DP en las partes del conjunto de estados que son más relevantes para el agente. Este tipo de enfoque es un tema recurrente en el aprendizaje por refuerzo.

La iteración de políticas consiste en dos procesos simultáneos que interactúan entre sí: uno hace que la función de valor sea coherente con la política actual (evaluación de la política) y el otro hace que la política sea codiciosa con respecto a la función de valor actual (mejora de la política). En la iteración de políticas, estos dos procesos se alternan, y cada uno se completa antes de que comience el otro, pero esto no es realmente necesario. En la iteración de valor, por ejemplo, solo se realiza una única iteración de evaluación de políticas entre cada mejora de políticas. En los métodos de DP asincrónicos, los procesos de evaluación y mejora se intercalan con un nivel de detalle aún más fino. En algunos casos, se actualiza un solo estado en un proceso antes de volver al otro. Mientras ambos procesos sigan actualizando todos los estados, el resultado final suele ser el mismo: convergencia a la función de valor óptima y una política óptima.

Utilizamos el término iteración de políticas generalizadas (GPI) para referirnos a la idea general de permitir que los procesos de evaluación y mejora de políticas interactúen, independientemente de la granularidad y otros detalles de los dos procesos.

Casi todos los métodos de aprendizaje por refuerzo se describen bien como GPI. Es decir, todos tienen políticas y funciones de valor identificables, y la política siempre se mejora con respecto a la función de valor y la función de valor siempre se dirige hacia la función de valor para la política, como lo sugiere el siguiente diagrama. Si tanto el proceso de evaluación como el proceso de mejora se estabilizan, es decir, ya no producen cambios, entonces la función de valor y la política deben ser óptimas. La función de valor se estabiliza solo cuando es coherente con la política actual, y la política se estabiliza solo cuando es codiciosa con respecto a la función de valor actual.

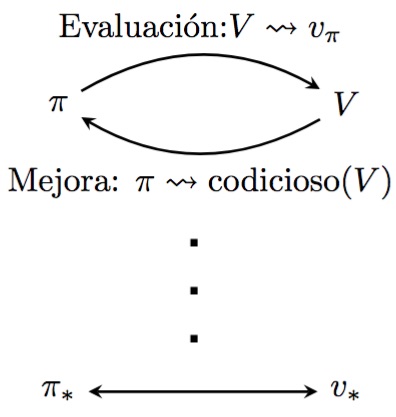
Los procesos de evaluación y mejora en la GPI pueden considerarse como procesos que compiten y cooperan entre sí. Compiten en el sentido de que tiran en direcciones opuestas. Hacer que la política sea codiciosa con respecto a la función de valor normalmente hace que la función de valor sea incorrecta para la política modificada, y hacer que la función de valor sea coherente con la política normalmente hace que la política ya no sea codiciosa. Sin embargo, a largo plazo, estos dos procesos interactúan para encontrar una única solución conjunta: la función de valor óptima y una política óptima.